研究内容

グラフ理論に基づく格子上の場の理論の理解

格子上の場の理論とは時空間を離散化（格子化）し、格子点やそれらを繋ぐ線上に自由度を定義することで、数学的に場の量子論を定式化する理論です。この理論は、モンテカルロ法と呼ばれる統計的手法を用いた数値計算が有効であり、多くの成果を上げています。一方で、時空間を離散化したことによって重大な問題が生じることもあります。そこで、我々は格子上の場の理論をグラフ理論として捉え直し、格子理論の諸々の問題をグラフ理論の問題に焼き直すことで格子理論への新しい知見の獲得を試みています。ここで補足しますと、グラフ理論とは点と辺で構成されるグラフに関する数学の理論です。

関係する主な業績：
J.Yumoto, T.Misumi, JHEP02(2022)104

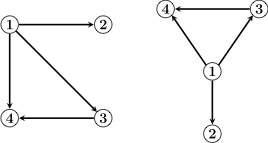
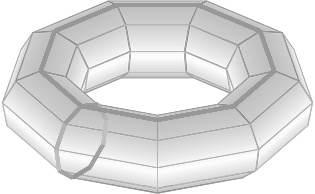
位相幾何学的視点に基づく格子fermionの研究

格子上の場の理論においてフェルミオンを素朴に格子化する、すなわちディラック場の作用を必要な対称性を要請したまま離散化すると余分な自由度（species）が出現するという「フェルミオン・ダブリング」と呼ばれる問題が生じます。よく知られた結果として、周期的境界条件を課した\(4\)次元正方格子（\(4\)-d torus）上において最大で\(2^4\)個のspeciesが出現することが知られています。しかし、これまで一般にspeciesの個数については判っていませんでしたが、背景時空に依存する位相不変量とspeciesの最大個数が一致するという証拠が多数見つかっており、我々は多様体を離散化した格子上のspeciesの最大個数について、その多様体の位相不変量(Betti数)を用いた予想を立て、その証明を試みています。

関係する主な論文：
J.Yumoto, T.Misumi, [arXiv:2301.09805]